【导读】2020安徽农商行社会招聘公告暂未发布，笔试时间为公告发布后的一个月之后。力锐教育为大家整理了2020安徽农商行校园招聘公告|职位表|报名时间|报名入口|考试时间备考专题，考生可提前收藏专题页面，我们在公告发布第一时间同步更新，更多关于2020安徽农商行招聘备考信息可关注力锐教育。

极值问题在行测数学运算中被考察的几率很大，这类题目的解答方法比较多，对这类知识的考查也有可能会成为近几年的重点。下面力锐教育专家就讲解一下均值不等式解极值问题的应用。

一、什么是均值不等式

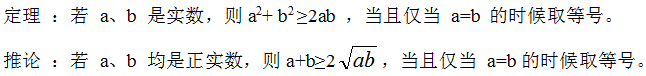
二、均值不等式的应用

1、和一定，求积最大。

由上述推论可知，当正实数a、b的和为定值时，a与b的乘积可取到最大值，当且仅当a=b时取到。

【试题再现】某苗木公司准备出售一批苗木，如果每株以4元出售，可卖出20万株，若苗木单价每提高0.4元，就会少卖10000株。问在最佳定价的情况下，该公司最大收入是多少万元?

A.60 B.80 C.90 D.100

【答案】C。安徽农商行招聘网解析：总收入=售价×销量。设最佳定价在4元每株的基础上提高0.4x元，则销量会在20万株的基础上少卖x万株故。收入=(4+0.4x)×(20-x)=0.4(10+x)×(20-x)。求收入的最大值，即求(10+x)×(20-x)的最大值。因为(10+x)+(20-x)=30，即(10+x)与(20-x)的和一定，当且仅当10+x=20-x，x=5时，(10+x)×(20-x)取到最大值(10+5)×(20-5)=225，故公司最大收入为0.4×225=90万元，选C。

2、积一定，求和最小。

由上述推论可知，当正实数a、b的乘积为定值时，a与b的和可取到最小值，当且仅当a=b时取到。

【试题再现】某村民要在屋顶建造一个长方体无盖贮水池，如果池底每平方米的造价为150元，池壁每平方米的造价为120元，那么要造一个深为3米容积为48立方米的无盖贮水池最低造价是多少元?

A.6460 B.7200 C.8160 D.9600

【答案】C。安徽农商行招聘网解析：水池造价=池地造价+池壁造价。水池深3米、容积48米，设长和宽分别为a、b，有底面积ab=48&pide;3=16平方米，池壁面积为2×(3a+3b)。因此水池造价为：16×150+2×(3a+3b)×120=2400+720×(a+b)。要求水池最低造价，即求a+b的最小值。a、b积一定为16，和a+b可取得最小值，且a=b=4时取到。因此，最低造价为2400+720×(4+4)=2400+5760=8160元，选C。

安徽农商行考试交流群：529852728

咨询QQ：1927004227

银行/安徽农商行考试复习综合教材

力锐教育官方微信公众号